BlueNote's Real-time Phase Vocoder
I recently launched an app called BlueNote. It’s essentially a fancy audio player that helps you learn music by ear. The most obvious way to learn music by ear is to slow down the audio to make it easier to hear the notes and rhythms.
Several different approaches exist for changing the playback speed of audio without changing the pitch, namely the phase vocoder originally proposed in 1966. Phase vocoder output quality can vary depending on the harmonic content of the audio (for example, slowed percussion sounds worse than piano or guitar). But for our purposes, the phase vocoder is more than good enough. We don’t need top notch quality; we just need to be able to hear the notes clearly enough to transcribe them.
Conveniently, Apple provides a phase vocoder implementation in the form of AVAudioUnitTimePitch. It’s pretty easy to use in practice:
func setupAudio() {
let format = AVAudioFormat(standardFormatWithSampleRate: Double(sampleRate), channels: 2)
let srcNode = AVAudioSourceNode { _, _, frameCount, audioBufferList -> OSStatus in
// Audio render callback
return noErr
}
let engine = AVAudioEngine()
let timePitch = AVAudioUnitTimePitch()
engine.attach(srcNode)
engine.attach(timePitch)
engine.connect(srcNode, to: timePitch, format: format)
engine.connect(timePitch, to: engine.outputNode, format: format)
try? engine.start()
timePitch.rate = 0.5
}But I wanted to take things a step further. What if you could slow down the audio to a standstill and “freeze” at any point? Imagine being able to sustain a piano chord forever, pick out the individual notes, and then move on to the next chord.
Here’s what that sounds like in the finished app:
We can’t accomplish this effect with Apple’s AVAudioUnitTimePitch – the minimum playback rate is 1/32. We want a rate of 0. Are there other ways to freeze audio? Let’s review some possible approaches.
Granular synthesis
One of the simplest freezing approaches is a granularizer – an algorithm that plays back small chunks of audio repeatedly. Given a playhead position in an audio file, we could grab a small chunk of the audio at that point:
Let’s try looping this chunk:
Not exactly what we’re going for. Looping a chunk of audio results in discontinuities at the loop boundaries, which sounds like a harsh click:
With small chunk sizes, clicks occur rapidly and make the original audio unintelligible.
Windowing
A simple improvement is applying a windowing function to the audio chunk before we loop it. A common window is the Hamming function:
Before looping our audio chunk, we’ll multiply it by this window like so:
This gets rid of the clicks, but the audio still sounds strange because it’s rapidly increasing and decreasing in volume:
To fix this, we can overlap our windowed chunks before we add them back together. The Hamming function has a nice property called Constant Overlap Add (COLA), meaning that when multiple windows are added together with a 50% overlap (factor of 2), the result is a straight line with a slope of zero, plus fades in and out:
This means our output audio should have a constant volume as long as we use a 2x overlap.
Here’s what our looped audio looks like with overlapping windows:
Visually, the output looks great. It doesn’t have any discontinuities and the volume looks constant. Here’s what that sounds like:
Not great. There’s a low frequency hum and the audio sounds different than the original. This becomes more obvious at different playhead positions. Listen to just how different the “frozen” audio sounds compared to normal playback:
Why is this? The output audio should be smooth, right?
Not quite. Even though the output looks fine visually, human ears are incredibly sensitive to timbre. The looped audio is windowed and added, so it has no discontinuities or changes in volume. But because we’re looping the same thing over and over, it still has an implicit periodicity that manifests as artifacts. At a sample rate of 44100 and a chunk size of 1024 with an overlap of 2, we will hear a repetition of the chunk every (1024/2)/44100 = 0.012 s, resulting in a 1/0.012 = 86 Hz artifact. And constructive and destructive interference created in the overlapping and adding process creates an ugly mess of additional frequency components, none of which were present in the original audio. Using a high pass filter on the output doesn’t do much good – the artifacts are too sparse and unpredictable to filter out.
It should be obvious by now that we need a different approach. The phase vocoder works well for slowing down audio, but remember Apple’s implementation has a minimum rate of 1/32. Let’s explore how we can write our own phase vocoder that resynthesizes audio in realtime, resulting in a rate of 0 and letting us scrub and freeze the audio at any position.
How phase vocoders work
The heart of our phase vocoder implementation is the Short Time Fourier Transform (STFT). Performing an STFT on a chunk of audio splits it into a series of sine wave components (bins), each having its own magnitude and phase. The frequencies of the sine waves are spaced at regular intervals according to the duration of the input audio chunk. It’s sort of like unbaking a cake so we can take a look at the original ingredients and their quantities. In this case, the ingredients are pure sine waves, along with information about how loud they are (magnitude) and their position in time (phase). Once “unbaked”, we can add the sine waves back together to reconstruct the original chunk of audio (an inverse STFT).
The neat thing about this approach is that we can modify the ingredients before rebaking the cake, allowing us to synthesize new cakes with different properties. This pipeline is the fundamental basis for a wide variety of signal processing tasks.
The phase of each bin is its offset in time normalized to the bin frequency, expressed in radians. In most STFT implementations, phases are “unwrapped” between -π and π. This means that as phases increase, they jump back around to -π once they exceed π. The same principle applies for subtracting phases. Adding 2π (a full cycle in radians) to a phase and unwrapping produces the original phase. This makes sense – if you shift a sine wave forward horizontally by one cycle, you’ll end up with the original sine wave.
Windowing – Part 2
Before performing an STFT, we need to window our audio chunk using a Hamming window. The STFT calculates component sine waves for an input sequence that is infinitely long. When we feed a finite chunk of audio into the algorithm, the algorithm effectively assumes the chunk is looped infinitely. If you want to know more about the math behind this, check out 3Blue1Brown’s video.
Remember the clicks we got from our first time domain approach? Those clicks were the result of discontinuities at loop boundaries. When fed through an STFT, clicks manifest strongest in high frequency components. A discontinuity is really just a momentary high frequency component. Unfortunately, this information bleeds into the entire spectrum and can’t be filtered out. The clicks do not reflect the original audio; they’re added artifacts as a result of discontinuous looping. Windowing removes the clicks and ensures smooth loop boundaries, resulting in accurate magnitudes and phases.
Resynthesis
Once we’ve performed an STFT on a windowed audio chunk, we want to modify the magnitudes and phases, synthesize a new chunk, and add it to a buffer that will be consumed during playback. Every time we bake a new chunk, we should first modify the ingredients such that the new chunk fits like a puzzle piece after the previous chunk. We’re taking the signature of the original audio chunk and using it to create an infinite continuation. No discontinuities, no volume changes, and no periodicity. This is a simplified explanation but it should give you an idea of what we’re trying to accomplish.
It makes sense to hold magnitudes constant – why change the volume of each sine wave? We want to change the phase. Phases for each bin should be updated at every resynthesis step according to the expected phase change over the duration of a chunk. That way, each component sine wave is a continuation of the corresponding sine wave in the previous chunk. When we add all the sine waves back together, since they’re all perfect continuations, the new baked chunk should also be a perfect continuation of the previous chunk.
Since we know the frequency of each bin, we can calculate the expected phase change of a sine wave at that frequency over the duration of one chunk. The expected phase change is:
We’re taking the duration of a chunk in seconds (chunkSize / sampleRate) and multiplying it by the bin frequency in Hz, which you can think of as cycles / second. This gives us the phase change in cycles, which gets scaled by 2π to convert to radians.
But wait! Our audio is windowed and overlapped, so we need to use a 2x overlap during resynthesis. This means we should calculate the expected phase change over chunkSize / 2:
We can store the current phases for each bin in an array. At each new resynthesis step, we’ll increment the phases according to Δɸ and then unwrap the result so it’s between -π and π. Then we’ll use those new phases along with the original magnitudes to bake a new chunk of audio. We’ll have to overlap this new chunk with the previous chunk like we did before.
Here’s some pseudocode to illustrate the pipeline so far:
let FFT_SIZE = 1024
let SAMPLE_RATE = 44100
let OVERLAP = 2
var phaseAccumulator: [Float] = [Float](repeating: -100.0, count: FFT_SIZE/2)
var resynthesizedAudio: [Float] = []
func resynthesisStep() {
let chunk = getChunk(playheadPosition, FFT_SIZE)
let windowedChunk = hammingWindow(chunk)
let (mags, phases) = forwardFFT(windowedChunk)
for i in 0..<FFT_SIZE/2 {
if phaseAccumulator[i] == -100.0 {
// Initialize accumulated phases
phaseAccumulator[i] = phases[i]
} else {
// Accumulate phase
let expectedPhaseChange = (windowedChunk.count / OVERLAP) * (1 / SAMPLE_RATE) * binFreq * 2 * pi
phaseAccumulator[i] += expectedPhaseChange
phases[i] = phaseAccumulator[i]
}
}
resynthesizedChunk = inverseFFT(mags, phases)
overlapAndAdd(resynthesizedAudio, resynthesizedChunk, OVERLAP)
}Let’s hear what this sounds like:
Oh no, we’ve still got artifacts in the output! What went wrong here? Let’s see what each new chunk looks like individually:
The first chunk looks correct because it’s just the original chunk without any modified phases. But the windowing is broken on subsequent chunks, which creates discontinuities in the output, leading to clicks and artifacts. Modifying the phases broke the windowing. This makes sense; there’s no guarantee the resynthesized audio should have the exact same window envelope as the original. We modified the ingredients, so we got a slightly different cake.
But we still want the overall output to be continuous. An obvious thing to try is windowing the output before adding it to the output buffer. Here’s what that looks like in pseudocode (bolded text changed):
let FFT_SIZE = 1024
let SAMPLE_RATE = 44100
let OVERLAP = 2
var phaseAccumulator: [Float] = [Float](repeating: -100.0, count: FFT_SIZE/2)
var resynthesizedAudio: [Float] = []
func resynthesisStep() {
let chunk = getChunk(playheadPosition, FFT_SIZE)
let windowedChunk = hammingWindow(chunk)
let (mags, phases) = forwardFFT(windowedChunk)
for i in 0..<FFT_SIZE/2 {
if phaseAccumulator[i] == -100.0 {
// Initialize accumulated phases
phaseAccumulator[i] = phases[i]
} else {
// Accumulate phase
let expectedPhaseChange = (windowedChunk.count / OVERLAP) * (1 / SAMPLE_RATE) * binFreq * 2 * pi
phaseAccumulator[i] = unwrap(phaseAccumulator[i] + expectedPhaseChange)
phases[i] = phaseAccumulator[i]
}
}
resynthesizedChunk = inverseFFT(mags, phases)
let windowedResynthesizedChunk = hammingWindow(resynthesizedChunk)
overlapAndAdd(resynthesizedAudio, windowedResynthesizedChunk, OVERLAP)
}
Let’s hear what that sounds like:
Better! But it’s still a bit off. The volume envelope seems to be changing rapidly, creating a fluttering effect. Because we’re applying the window twice, we’ve broken the Constant Overlap Add property. Applying the window at input and output results in a squared window, which does not add up to 1 with a 2x overlap:
We can recover the COLA property if we use a 4x overlap. This is an important piece of the puzzle. Squared Hamming windows will add up to 1 if overlapped by a factor of 4:
Since we’re changing the overlap amount, we need to update our phase accumulation function to account for that:
Here’s our current pseudocode (bolded text changed):
let FFT_SIZE = 1024
let SAMPLE_RATE = 44100
let OVERLAP = 4
var phaseAccumulator: [Float] = [Float](repeating: -100.0, count: FFT_SIZE/2)
var resynthesizedAudio: [Float] = []
func resynthesisStep() {
let chunk = getChunk(playheadPosition, FFT_SIZE)
let windowedChunk = hammingWindow(chunk)
let (mags, phases) = forwardFFT(windowedChunk)
for i in 0..<FFT_SIZE/2 {
if phaseAccumulator[i] == -100.0 {
// Initialize accumulated phases
phaseAccumulator[i] = phases[i]
} else {
// Accumulate phase
let expectedPhaseChange = (windowedChunk.count / OVERLAP) * (1 / SAMPLE_RATE) * binFreq
phaseAccumulator[i] = unwrap(phaseAccumulator[i] + expectedPhaseChange)
phases[i] = phaseAccumulator[i]
}
}
resynthesizedChunk = inverseFFT(mags, phases)
let windowedResynthesizedChunk = hammingWindow(resynthesizedChunk)
overlapAndAdd(resynthesizedAudio, windowedResynthesizedChunk, OVERLAP)
}And let’s hear what it sounds like:
This is still pretty far off from what we want.
Side note: windowing the output is also handy because it lets us update the playhead position whenever we want without creating any discontinuities in the output audio. Everything gets crossfaded smoothly. This lets us scrub around the file and hear what it sounds like in real time.
True frequencies
I’m actually a bit hesitant to call this a phase vocoder because the implementation differs in one key regard. A traditional phase vocoder calculates phase changes for every bin according to the “true frequency” of that bin.
When we perform an STFT, the frequencies of each bin are spaced at regular intervals according to the input duration. For a chunk size of 1024 with a 44100 sample rate, the bin frequency spacing will be 44100/1024 ≅ 43.07 Hz. So the bin frequencies are:
Bin 1 ------------- 43.07 Hz
Bin 2 ------------- 86.13 Hz
Bin 3 ------------ 129.20 Hz
Bin 4 ------------ 172.27 Hz
...
Bin 511 -------- 22006.93 Hz
Bin 512 -------- 22050.00 Hz In real world audio, the probability that the actual frequency components line up perfectly with the bin frequencies is basically zero. True component frequencies will always lie somewhere between bin frequencies, and theoretically there may be infinitely many actual components. The STFT losslessly compresses this information into discrete bins, preserving everything required to resynthesize the original audio. Information that’s present between bin frequencies gets smeared out across multiple adjacent bins.
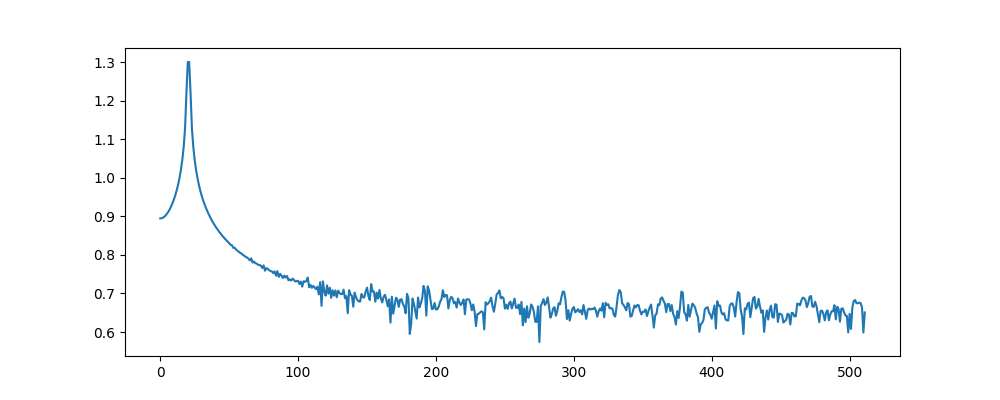
This can be easier to conceptualize by looking at a simple input signal. We’ll assume the input is a single sine wave at 882.86 Hz (halfway between bins 20 and 21):
Here’s what the magnitude spectrum for that chunk looks like. Notice the smearing effect:
The STFT represents a 882.86 Hz sine wave by using the surrounding bins, with smaller magnitudes in proportion to the distance from bins 20-21.
This post by William Sethares and this post by Stephan Bernsee are great deep dives into how true bin frequencies are calculated in a traditional phase vocoder. TLDR – there are different schools of thought on this, ranging from peak picking to a phase gradient estimation approach proposed in 2022.
Our resynthesis algorithm is using quantized bin frequencies to calculate expected phase changes. As a result, the output audio will likely have different timbral qualities than the input. To make the output sound better, we should use the true bin frequencies to calculate expected phase changes. Normally, calculating the true bin frequencies is an intermediate step that helps us calculate better expected phase changes. But we can skip the true frequency calculation step and simplify our pipeline if we’re willing to use a bit more compute and perform a second STFT. Here’s how that works:
The smearing effect causes bin phases to change with respect to time to compensate for the difference in true vs bin frequencies. The rate of change will differ from the theoretical Δɸ we calculated earlier, which assumes the true frequencies align perfectly with the bin frequencies.
One way we can estimate the instantaneous rate of phase change is by calculating the phase difference with respect to time between the chunk at the playhead position and a chunk that occurred some Δt ago. We want the derivative of the phases at the playhead. Doing this in code is as simple as calculating another STFT at a playhead offset of -1. We can then use this rate of phase change to calculate the expected phase change at the next chunk overlap.
Here’s the final pseudocode:
let FFT_SIZE = 1024
let SAMPLE_RATE = 44100
let OVERLAP = 4
var phaseAccumulator: [Float] = [Float](repeating: -100.0, count: FFT_SIZE/2)
var resynthesizedAudio: [Float] = []
func resynthesisStep() {
let chunk = getChunk(playheadPosition, FFT_SIZE)
let prevChunk = getChunk(playheadPosition - 1, FFT_SIZE)
let windowedChunk = hammingWindow(chunk)
let windowedPrevChunk = hammingWindow(prevChunk)
let (mags, phases) = forwardFFT(windowedChunk)
let (prevMags, prevPhases) = forwardFFT(windowedPrevChunk)
for i in 0..<FFT_SIZE/2 {
if phaseAccumulator[i] == -100.0 {
// Initialize accumulated phases
phaseAccumulator[i] = phases[i]
} else {
// Accumulate phase
let expectedPhaseChange = (phases[i] - prevPhases[i]) * (windowedChunk.count / OVERLAP)
phaseAccumulator[i] = unwrap(phaseAccumulator[i] + expectedPhaseChange)
phases[i] = phaseAccumulator[i]
}
}
resynthesizedChunk = inverseFFT(mags, phases)
let windowedResynthesizedChunk = hammingWindow(resynthesizedChunk)
overlapAndAdd(resynthesizedAudio, windowedResynthesizedChunk, OVERLAP)
}And here’s what the final algorithm sounds like:
Conclusion
This was a deep dive into the DSP behind a real-time phase vocoder implementation. I’ve skipped a bunch of parts – DSP and non-DSP related – needed to make the actual app function.
If you’re curious, take a look at the BlueNote source code here. The full implementation of this algorithm is in ScrubbingResynthesis.swift.
Download the app on the App Store here.
Hope you enjoyed. Leave a comment and let me know what you think!